MeDiaN@Sports - « L’Énergie cinétique à vélo »

2010
10.10

MeDiaN@Sports – « L’Énergie cinétique à vélo »

Catégorie: .MeDiaN@Sports / Tags: aucun tag / Ajouter un commentaire

Présentation générale

Dans cet article, je me suis amusé à déterminer l’énergie cinétique d’un vélo lorsque celui-ci suit une trajectoire rectiligne. L’idée était de vérifier que le changement des roues de mon Gitane pour des Mavic Ksyrium Elite était bien la bonne solution pour améliorer son comportement.

Modélisation du problème

Système isolé

On choisit d’isoler les éléments les plus significatifs du vélo, c’est à dire les composants tournant et/ou ayant une masse importante : cycliste, cadre avec les éléments qui lui sont liés et en fixant la fourche, roues (avant et arrière), pédalier.

Schématisation

Description

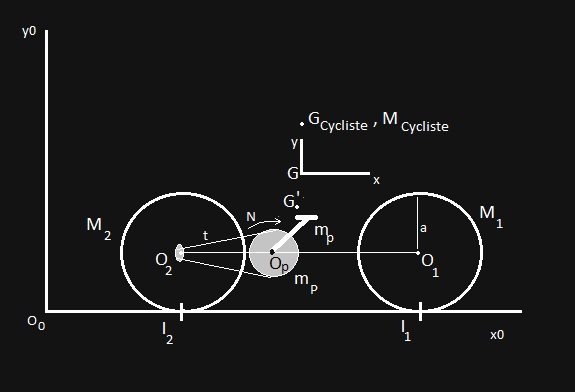
Le vélo est schématisé par le système de centre d’inertie G tel que :

– Cadre, éléments fixes forme un solide S de masse M et dont le centre de gravité G’ est positionné en [b, c, 0] dans le repère R.

– Les roues avant $S _{1}$ et arrière $S _{2}$ sont des cercles de rayon a et de masses $M _{1}$ et $M _{2}$ uniformément répartie sur la circonférence. Les frottements sont négligés. $O _{1}$ en [d,e,0] et $O _{2}$ en [f,e,0].

-Le pédalier $S _{P}$ de masse $m _{P}$ munie de ses pédales $m_{p}$ de masse $S _{p}$ . $O_{P}$ en [g,h,0]

-Le cycliste $S _{Cycliste}$ de masse $M _{Cycliste}$ . $G_{Cycliste}$ en [i,j,0]

Bilan des paramètres

4 paramètres :

$\theta _{1}$ : Angle de rotation de la roue avant;

$\theta _{2}$ : Angle de rotation de la roue arrière;

$\theta _{p}$ : Angle de rotation du pédalier;

$\xi :$ Abscisse de G dans $\left ( O_{0},\vec{x_{0}},\vec{y_{0}} \right )$

Résolution

Détermination des paramètres indépendants

3 Équations de liaison (roulement sans glissement et transmission par chaîne)

– Roue avant : $\vec{V_{\left ( I\in S_{1}/R_{0} \right )}}=\vec{0}$ <=> $\vec{V_{\left (O{_{1}/R_{0}}\right)}}+\Omega _{S_{1}/R_{0}}\wedge \vec{O_{1}I_{1}}=\vec{0}$

$\vec{V_{\left ( I\in S_{1}/R_{0} \right )}}=\left ( \dot{\xi}+a\dot{\theta _{1}} \right ).\vec{x_{0}}$

– Roue arrière : $\vec{V_{\left ( I\in S_{2}/R_{0} \right )}}=\vec{0}$ <=> $\vec{V_{\left (O{_{2}/R_{0}}\right)}}+\Omega _{S_{2}/R_{0}}\wedge \vec{O_{2}I_{2}}=\vec{0}$

$\vec{V_{\left ( I\in S_{2}/R_{0} \right )}}=\left ( \dot{\xi}+a\dot{\theta _{2}} \right ).\vec{x_{0}}$

– Transmission : Soit t le facteur de transmission : $t=\frac{\dot{O_{2}} }{\dot{O_{p}}}=\frac{Ndents_{plateau} }{Ndents_{pignon}}$

Comme elles ont le même diamètre, les 2 roues tournent à la même vitesse $\left ( \dot{O_{2}}=\dot{O_{1}} \right )$ . En connaissant t, on peut donc tout exprimer en fonction de la vitesse de rotation du pédalier:

$\mathbf{\dot{\theta _{1}}=\dot{\theta _{2}}=\frac{-\dot{\xi }}{a}=\dot{\theta_{p}}.t}$ (1) : une relation liant tous les paramètres

Relation en exprimant la vitesse de pédalage sous la forme d’une cadence :

On exprime traditionnellement la cadence de pédalage en tr/min alors que la relation ci-dessus est en rad/sec. Soit N la cadence de pédalage en tr/min, la conversion des unités donne :

$\dot{\theta _{1}}=\dot{\theta _{2}}=\frac{-\dot{\xi }}{a}=\frac{\pi .N.t}{30}$ (2)

Calcul de l’énergie cinétique du système

Je vais maintenant pouvoir écrire l’équation de l’énergie cinétique de mon vélo ramenée à ma cadence de pédalage uniquement. L’énergie cinétique totale est la somme des énergie propre à chacun des sous-ensembles composant le système.

$T = T\left ( S_{0}/R_{0} \right )+ T\left ( S_{1}/R_{0} \right )+T\left ( S_{2}/R_{0} \right )+T\left ( S_{P}/R_{0} +T\left ( Cycliste/R_{0} \right ) \right )$

Chaque énergie peut donc se calculer de manière indépendante.

– $S_{0}$ (S/E cadre+éléments fixes) : Cas d’un corps en translation.

$T\left ( S_{0}/R_{0} \right) =\frac{1}{2}.M.\left [ \vec{V_{\left ( G_{0}\in S_{0}/R_{0} \right )}} \right ]^{2} +0 = \frac{1}{2}.M. \dot{\xi}^{2}$

– $S_{1}$ (S/E roue avant) : Cas d’un corps en translation et rotation simultanée.

$T\left ( S_{1}/R_{0} \right) =\frac{1}{2}.M_{1}.\left [ \vec{V_{\left ( O_{1}\in S_{1}/R_{0} \right )}} \right ]^{2} +\frac{1}{2}.\vec{\Omega \left ( S_{1}/R_{0}\right )}.\vec{\sigma \left ( O_{1}\in S_{1}/R_{0} \right )}$ avec $\vec{\sigma \left ( O_{1}\in S_{1}/R_{0} \right)}=\bar{I_{O_{1}}}.\vec{\Omega \left ( S_{1}/R_{0}\right )}$

or la matrice d’inertie pour un anneau tournant autour de l’axe orthogonal à son plan et passant par son centre est $\bar{I_{O_{1}}} =\begin{pmatrix}\frac{mR}{2}^{2} & 0 &0 \\0 &\frac{mR}{2}^{2}&0\\0&0&mR^{2}\end{pmatrix}$

donc $T\left ( S_{1}/R_{0}\right)= \frac{1}{2} M_{1}. \dot{\xi}^{2}+\frac{1}{2}. M_{1}.a^{2}.\dot{\theta _{1}^{2}}$

– $S_{2}$ (S/E roue arrière) : Idem.

$T\left ( S_{2}/R_{0}\right)= \frac{1}{2} M_{2}. \dot{\xi}^{2}+\frac{1}{2}. M_{2}.a^{2}.\dot{\theta _{2}^{2}}$

– $S_{2}$ (S/E Pédalier + Pédales) :

Le rayon de giration du sous ensemble est approximé à 13 cm, avec $m_{P}$ la masse du pédalier et $m_{p}$ la masse d’une pédale. Comme pour les roues, on a :

$T\left ( S_{p}/R_{0}\right)= \frac{1}{2} \left ( m_{P}+2.m_{p}\right) . \dot{\xi}^{2}+\frac{1}{2}. \left ( m_{P}+2.m_{p}\right).0.13^{2}.\dot{\theta _{p}^{2}}$

– $S_{Cycliste}$ (S/E Cycliste) :

$T\left ( S_{Cycliste}/R_{0} \right) =\frac{1}{2}.M_{Cycliste}. \dot{\xi}^{2}$

L’énergie cinétique totale du système est donc la suivante :

$T = \frac{1}{2} \left (\left ( M+M_{1}+M_{2}+m_{P}+2.m_{p}+M_{Cycliste} \right) . \dot{\xi}^{2} \right)$

$+\frac{1}{2} \left ( a^{2} \left ( M_{1}\dot{\theta _{1}^{2}}+M_{2}\dot{\theta _{2}^{2}} \right) +.0,13^{2} \left ( m_{P}+2.m_{p}\right) .\dot{\theta _{p}^{2}} \right)$

Les relations (1) et (2) permettent de simplifier cette expression en ramenant l’énergie cinétique à la rotation du pédalier. L’énergie cinétique totale peut ainsi être écrite sous la forme :

$T = \frac{1}{2} . K . \dot{\theta _{p}^{2}}=\frac{1}{2} . K \left (\frac{\pi . N}{30} \right)^{2}$ avec inertie équivalente ramenée au pédalier $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$

L’énergie cinétique d’un cycliste dépend donc principalement de sa masse, de celle de son vélo et de sa vitesse (qui est elle même fonction de la cadence de pédalage (N) et du braquet utilisé (t)). On remarque également que les roues comptent double dans ce calcul, et c’est pourquoi il vaut mieux privilégier un gain de poids sur les roues plutôt que sur un cadre pour upgrader son vélo.