MeDiaN@Sports - « L'Equation de mouvement à vélo »

2010
11.06

MeDiaN@Sports – « L’Equation de mouvement à vélo »

Catégorie: .MeDiaN@Sports / Tags: aucun tag / Ajouter un commentaire

Présentation générale

Dans cet article précédent, nous avons établis la relation donnant l’énergie cinétique d’un cycliste se déplaçant en ligne droite.

Rappel : $T = \frac{1}{2} . K . \dot{\theta _{p}^{2}}=\frac{1}{2} . K \left (\frac{\pi . N}{30} \right)^{2}$ avec inertie équivalente ramenée au pédalier $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$

En se basant sur le résultat de ce calcul, nous allons maintenant cherché à établir grâce aux multiplicateurs de Lagrange l’équation du mouvement régissant le déplacement de ce même vélo le long d’une pente.

Modélisation du problème

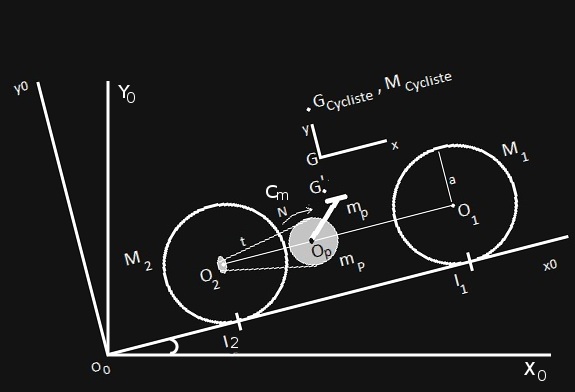
Schématisation

Description

Un vélo de centre de gravité G (en $[\xi , \nu, 0])$ avance le long d’une pente formant un angle $\alpha$ avec l’horizontale dans les mêmes conditions que celles énoncées dans l’article précédent.

Résolution

Equation de liaison

$\dot{\theta _{1}}=\dot{\theta _{2}}=\frac{-\dot{\xi }}{a}=\dot{\theta_{p}}.t=\frac{\pi .N.t}{30}$

Calcul des multiplicateurs de Lagrange : Qi

Comme tous les paramètres dépendent de $\theta_{p}$ , on exprimera tous les multiplicateurs en fonctions de cette même variable pour simplifier les dérivations à venir.

Pesanteur :
- Pour le cadre : $\vec{O_{o}G^{\prime}} = \vec{OG}+\vec{GG^{\prime}}=\xi.\vec{xo}+\mu.\vec{yo}+b.\vec{x}+c.\vec{y}$ et comme ( $\vec{x}//\vec{xo}$ ), $\vec{O_{o}G^{\prime}}=\left (\xi+b \right )\vec{xo}+\left (\mu+c\right )\vec{yo}$ .
  Dans Rg, on a
  $\vec{xo}=cos(\alpha).\vec{X0}+sin(\alpha).\vec{Yo}$ et $\vec{yo}=-sin(\alpha).\vec{X0}+cos(\alpha).\vec{Yo}$ .
  Donc
  $\vec{O_{o}G^{\prime}}.\vec{Yo} = \left (\xi+b \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)}$
  Finalement
  $V_{cadre} =M.g . \left [ \left (\xi+b \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)} \right ]+C^{te}$
  et en fonction de $\theta_{p}$ :
  $V_{cadre} =M.g . \left [ \left (a.t.\theta_{p}+b+k \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)} \right ]+C^{te}$
  
  Coefficient de Lagrange : $\left (Q_{cadre}\right )_\theta= -\frac{\partial V_{cadre} }{\partial \theta }=-M.g.a.t.sin{\alpha }$
- Pour la roue avant : $\vec{O_{o}O_{1}} = \vec{OG}+\vec{GO_{1}}=\xi.\vec{xo}+\mu.\vec{yo}+d.\vec{x}+e.\vec{y}$
  De la même façon : $\left (Q_{Rav}\right )_\theta= -\frac{\partial V_{Rav} }{\partial \theta }=-M_{1}.g.a.t.sin{\alpha }$
- Pour la roue arrière : $\left (Q_{Rar}\right )_\theta= -\frac{\partial V_{Rar} }{\partial \theta }=-M_{2}.g.a.t.sin{\alpha }$
- Pour le pédalier : $\left (Q_{Pedalier}\right )_\theta= -\frac{\partial V_{Pedalier} }{\partial \theta }=-\left (m_{P}+2m_{p}\right ) .g.a.t.sin{\alpha }$
- Pour le cycliste : $\left (Q_{Cycliste}\right )_\theta= -\frac{\partial V_{Cycliste} }{\partial \theta }=-M_{Cycliste}.g.a.t.sin{\alpha }$
Finalement, $\left (Q_{Pesanteur}\right )_\theta= -\frac{\partial V_{total} }{\partial \theta }=-\left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste}\right ) .g.a.t.sin{\alpha }$
Actionneurs :
Finalement : $\left (Q_{cycliste/pedalier}\right )_\theta= -\frac{\partial P_{(cycliste/pedalier)}^{*} }{\partial \theta^{*} }=C_{m}-\lambda_{1} \dot{\theta_{p}}$
Liaisons : Les roulements constituant les moyeux des roues n’étant pas parfaits, il conduisent à des pertes par frottement. Comme ci-dessus, elles sont directement proportionnelles à la vitesse de rotation des roues à un facteur $\lambda_{2}$ près. On a donc :
$\left (Q_{moyeu_{roues}}\right )_\theta= -\frac{\partial P_{(moyeu_{roues})}^{*} }{\partial \theta^{*} }=-2. \lambda_{2} \dot{\theta_{1}}=-2. \lambda_{2} \dot{\theta_{p}}.t$

Bilan
$\left (Q_{Systeme}\right )_\theta = \left (Q_{Pesanteur}\right )_\theta + \left (Q_{cycliste/pedalier}\right )_\theta + \left (Q_{moyeu_{roues}}\right )_\theta$
$\left (Q_{Systeme}\right )_\theta = -\left (M_{tot} \right ) .g.a.t.sin(\alpha) + C_{m}-\lambda_{1} \dot{\theta_{p}} - 2. \lambda_{2} \dot{\theta_{p}}t$

Détermination de l’équation générale du mouvement

$\left (Q_{Systeme}\right )_\theta = \frac{\mathrm{d} }{\mathrm{d} t}\left ( \frac{\partial T}{\partial \dot{\theta_{p}}} \right )-\frac{\partial T}{\partial \theta_{p}}$ avec $\frac{\partial T}{\partial \dot{\theta_{p}}} = K \dot{\theta_{p}}$ et $\frac{\partial T}{\partial \theta_{p}} = 0$
D’où $\left (Q_{Systeme}\right )_\theta = K\ddot{\theta_{p} } - 0$
Finalement $-\left (M_{tot} \right ) .g.a.sin(\alpha) + C_{m}-\lambda_{1} \dot{\theta_{p}} - 2. \lambda_{2} \dot{\theta_{p}}t = K\ddot{\theta_{p} }$

Conclusion
$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha)$
Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$
$\alpha = Arctan (\frac{Denivele}{100})$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$

Le couple moteur que doit fournir le cycliste à vitesse constante en cote ( $\ddot{\theta_{p} }=0$ ) doit compenser l’effet de la pesanteur (qui sera d’autant plus important que la masse du cycliste+vélo sera élevée et la pente accentuée) ainsi que les différentes pertes dans la transmission et les roulements.

On constate également que l’inertie intervient quand à elle dès que le cycliste cherche à accélérer sa vitesse. Un vélo à faible inertie favorisera donc particulièrement les changements de rythme.

La vitesse maximale que l’on pourrait calculer à partir de cette équation serait toutefois gigantesque car l’équation ne prend absolument pas en compte l’action qu’exerce l’environnement sur le cycliste (résistance au roulement, facteurs aérodynamique,…).